PEtab Tutorial¶
Overview¶
In the following, we demonstrate how to set up a parameter estimation problem in PEtab based on a realistic application example. To this end, we consider the model and experimental data by Boehm et al. (2014). The model describes the dynamics of phosphorylation and dimerization of the transcription factors STAT5A and STAT5B. A visualization and the corresponding reactions of the model are provided below, although the details of the model are not relevant for the purpose of this tutorial. For more details, we refer to the original publication (Boehm et al., 2014).
A PEtab problem consists of 1) an SBML model of a biological system, 2) condition, observable and measurement definitions, and 3) the specification of the parameters. We will show how to generate the respective files in the following.
1. The model¶
PEtab assumes that an SBML file of the model exists. Here, we use the SBML model provided in the original publication, which is also available on Biomodels (https://www.ebi.ac.uk/biomodels/BIOMD0000000591). For illustration purposes we slightly modified the SBML model and shortened some parts of the PEtab files. The full PEtab problem introduced in this tutorial is available online.
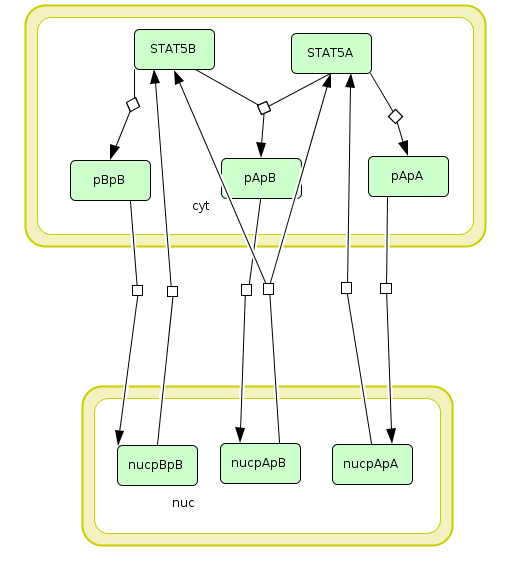
Visualization of the model used as example in this tutorial. The model describes the dynamics of phosphorylation and dimerization of the transcription factors STAT5A and STAT5B.
| ID | Reaction | Rate law |
|---|---|---|
| R1 | 2 STAT5A → pApA | cyt * BaF3_Epo * STAT5A^2 * k_phos |
| R2 | STAT5A + STAT5B → pApB | cyt * BaF3_Epo * STAT5A * STAT5B * k_phos |
| R3 | 2 STAT5B → pBpB | cyt * BaF3_Epo * STAT5B^2 * k_phos |
| R4 | pApA → nucpApA | cyt * k_imp_homo * pApA |
| R5 | pApB → nucpApB | cyt * k_imp_hetero * pApB |
| R6 | pBpB → nucpBpB | cyt * k_imp_homo * pBpB |
| R7 | nucpApA → 2 STAT5A | nuc * k_exp_homo * nucpApA |
| R8 | nucpApB → STAT5A + STAT5B | nuc * k_exp_hetero * nucpApB |
| R9 | nucpBpB → 2 STAT5B | nuc * k_exp_homo * nucpBpB |
2. Linking model and measurements¶
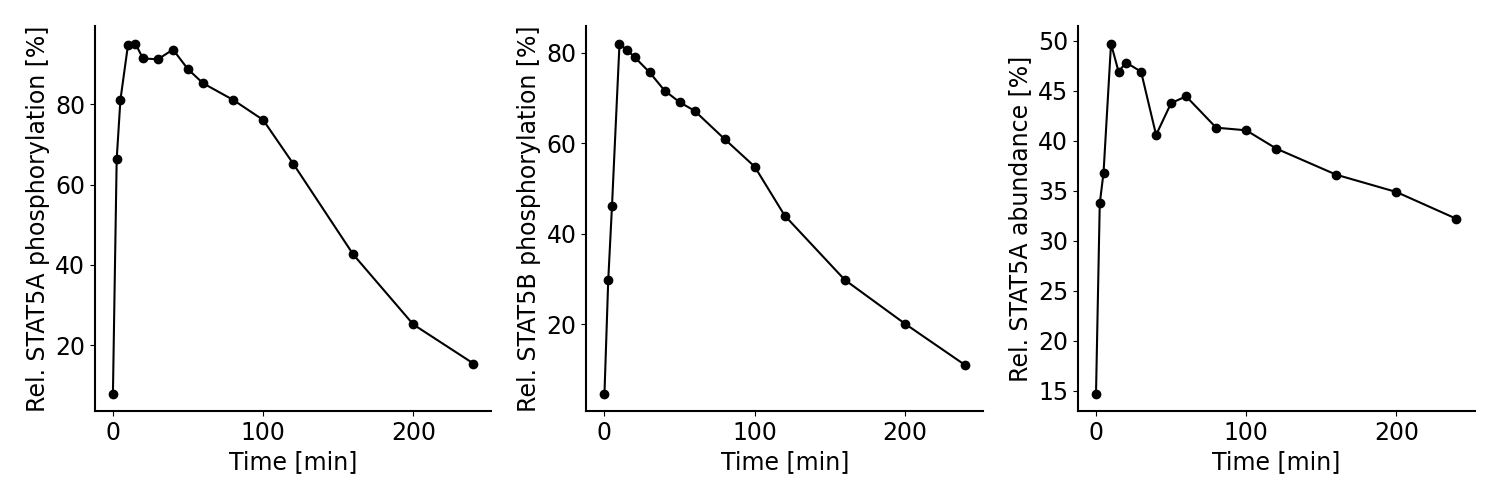
The model by Boehm et al. (2014) was calibrated on measurements on phosphorylation levels of STAT5A and STAT5B as well as relative STAT5A abundance for different timepoints between 0 - 240 minutes after stimulation with erythropoietin (Epo):
To define a parameter estimation problem in PEtab, we need to map measurements to the model states. To this end, we need to 1) specify the experimental conditions the measurements were generated from, 2) specify observation functions and error models, and 3) specify the measurements themselves. For this, we need to define observation functions as well as experimental conditions under which a measurement was performed.
2.1 Specifying experimental conditions¶
All measurements were collected under the same experimental condition, which is a stimulation with Epo. This is specified in the experimental condition PEtab file, a tab-separated values (TSV) file[1], by providing a condition identifier and listing all condition-specific parameters and their respective values.
In the problem considered here, the relevant parameter is
Epo_concentration which we want to set to a value of 1.25E-7, as the
only condition-specific parameter. Since in this example we include data from
only one single experiment, it would not be necessary to specify the condition
parameter here, but instead the value could have been also set in the model or
in the parameter table. However, the benefit of specifying it in the condition
table is, that it allows us to easily add measurements from other
experiments performed with different Epo concentrations later on.
The condition table looks as follows:
| conditionId | conditionName | Epo_concentration |
|---|---|---|
| epo_stimulation | Stimulation with 1.25E-7 Epo | 1.25E-7 |
- conditionId is a unique identifier to define the different conditions and link them to the measurements (see measurement file below). Additional measurements e.g. for different Epo concentrations can be defined by adding new rows.
- conditionName can be used as a human readable description of the condition e.g. for plotting.
The following column headers (here Epo_concentration) refer to different parameters or species in the model, the values of which are overridden by these condition-specific values. Here, we define the Epo concentration, but additional columns could be used to e.g. set different initial concentrations of STAT5A/B. In addition to numeric values, also parameter identifiers can be used here to introduce condition specific optimization parameters.
2.2 Specifying the observation model¶
To link the model states to the measured values, we specify observation functions. Additionally, a noise model can be introduced to account for the measurement errors. In PEtab, this can be encoded in the observable file:
| observableId | observableName | … |
|---|---|---|
| pSTAT5A_rel | Rel. STAT5A phosphorylation [%] | … |
| pSTAT5B_rel | Rel. STAT5B phosphorylation [%] | … |
| rSTAT5A_rel | Rel. STAT5A abundance [%] | … |
| … | observableFormula | … |
|---|---|---|
| … | 100*(2*pApA + pApB) / (2*pApA + pApB + STAT5A) | … |
| … | 100*(2*pBpB + pApB) / (2*pBpB + pApB + STAT5B) | … |
| … | 100*(STAT5A + pApB + 2*pApA) / (2 * pApB + 2* pApA + STAT5A + STAT5B + 2*pBpB) | … |
| … | noiseFormula | noiseDistribution |
|---|---|---|
| … | noiseParameter1_pSTAT5A_rel | normal |
| … | noiseParameter1_pSTAT5B_rel | normal |
| … | noiseParameter1_rSTAT5A_rel | normal |
- observableId specifies a unique identifier to the observables that can be used to link them to the measurements (see below).
- observableName can be used as a human readable description of the observable. Here, this corresponds to the y-label in the figure above.
- observableFormula is a mathematical expression defining how the model output is calculated. The formula can consist of species and parameters defined in the SBML file. In our example, we measure e.g. the relative phosphorylation level of STAT5A (pSTAT5A_rel), which is the sum of all species containing phosphorylated STAT5A over the sum of all species containing any form of STAT5A.
- noiseFormula is used to describe the formula for the measurement
noise. Together with noiseDistribution, it defines the noise model. In
this example, we assume additive, normally distributed measurement noise.
In this scenario,
noiseParameter1_{observableId}is the standard deviation of the measurement noise. Parameters following this naming scheme are expected to be overridden in a measurement-specific manner in the noiseParameters column of the measurement table (see below).
2.3 Specifying measurements¶
The experimental data is linked to the conditions via the conditionId and to the observables via the observableId. This is defined in the PEtab measurement file:
| observableId | simulationConditionId | measurement | time | noiseParameters |
|---|---|---|---|---|
| pSTAT5A_rel | epo_stimulation | 7.9 | 0 | sd_pSTAT5A_rel |
| … | … | … | … | … |
| pSTAT5A_rel | epo_stimulation | 15.4 | 240 | sd_pSTAT5A_rel |
| pSTAT5B_rel | epo_stimulation | 4.6 | 0 | sd_pSTAT5B_rel |
| … | … | … | … | … |
| pSTAT5B_rel | epo_stimulation | 10.96 | 240 | sd_pSTAT5B_rel |
| rSTAT5A_rel | epo_stimulation | 14.7 | 0 | sd_rSTAT5A_rel |
| … | … | … | … | … |
| rSTAT5A_rel | epo_stimulation | 32.2 | 240 | sd_rSTAT5A_rel |
- observableId references the observableId from the observable file.
- simulationConditionId references the conditionId from the experimental condition file.
- measurement defines the values that are measured for the respective observable and experimental condition.
- time is the time point at which the measurement was performed. For brevity, only the first and last time point of the example are shown here (the omitted measurements are indicated by “…” in the example).
- noiseParameters relates to the noiseParameters in the observables file. In our example, the measurement noise is unknown. Therefore we define parameters here which have to be estimated (see parameters sheet below). If the noise is known, e.g. from multiple replicates, numeric values can be used in this column.
3. Defining parameters¶
The model by Boehm et al. (2014) contains nine unknown parameters that need to be estimated from the experimental data. Additionally, it has two known parameters that are fixed to literature values.
The parameters file for this is given by:
| parameterId | parameterScale | lowerBound | upperBound | nominalValue | estimate |
|---|---|---|---|---|---|
| Epo_degradation_BaF3 | log10 | 1E-5 | 1E+5 | 1 | |
| k_exp_hetero | log10 | 1E-5 | 1E+5 | 1 | |
| k_exp_homo | log10 | 1E-5 | 1E+5 | 1 | |
| k_imp_hetero | log10 | 1E-5 | 1E+5 | 1 | |
| k_imp_homo | log10 | 1E-5 | 1E+5 | 1 | |
| k_phos | log10 | 1E-5 | 1E+5 | 1 | |
| ratio | lin | 0.693 | 0 | ||
| sd_pSTAT5A_rel | log10 | 1E-5 | 1E+5 | 1 | |
| sd_pSTAT5B_rel | log10 | 1E-5 | 1E+5 | 1 | |
| sd_rSTAT5A_rel | log10 | 1E-5 | 1E+5 | 1 |
- parameterId references parameters defined in the SBML file. Additionally, parameters defined in the measurement table can be used here. In this example, the standard deviations for the different observables (sd_{observableId}) are estimated.
- parameterScale is the scale on which parameters are estimated. Often, a logarithmic scale improves optimization. Alternatively, a linear scale can be used, e.g. when parameters can be negative.
- lowerBound and upperBound define the bounds for the parameters used during optimization. These are usually biologically plausible ranges.
- nominalValue are known values used for simulation. The entry can be left empty, if a value is unknown and subject to optimization.
- estimate defines whether the parameter is subject to optimization (1) or if it is fixed (0) to the value in the nominalValue column.
4. Visualization file¶
Optionally, a visualization file can be specified in PEtab which defines how the measurement data and potentially model simulations are plotted. So far, the visualization files are only supported by the PEtab Python library. Here, we describe a file that specifies the visualization of the measurement data similar to the figure above.
| plotId | plotTypeData | xLabel | yValues | yLabel |
|---|---|---|---|---|
| plot1 | MeanAndSD | Time [min] | pSTAT5A_rel | Rel. STAT5A phosphorylation [%] |
| plot2 | MeanAndSD | Time [min] | pSTAT5B_rel | Rel. STAT5B phosphorylation [%] |
| plot3 | MeanAndSD | Time [min] | rSTAT5A_rel | Rel. STAT5A abundance [%] |
- plotId corresponds to a specific plot. All lines which share the same plotId are combined into one plot.
- plotTypeData defines the plotting style of the measurement data. Here, we use mean and (if available) standard deviations.
- xLabel and yLabel are the labels of the x- and y-axes for the corresponding plot.
- yValues defines what is plotted. In this example the different observables are plotted individually.
There are various ways of further individualizing the plots, e.g. by defining legend entries or data plotted on log-scale (see the documentation for further information https://petab.readthedocs.io/en/latest/documentation_data_format.html#visualization-table).
5. YAML file¶
To group the previously mentioned PEtab files, a YAML file can be used,
defining which files constitute a PEtab problem. While being optional,
this makes it easier to import a PEtab problem into tools, and allows
reusing files for different PEtab problems. This file has the following
format (Boehm_JProteomeRes2014.yaml):
format_version: 1
parameter_file: parameters.tsv
problems:
- condition_files:
- experimental_conditions.tsv
measurement_files:
- measurement_data.tsv
observable_files:
- observables.tsv
sbml_files:
- model_Boehm_JProteomeRes2014.xml
visualization_files:
- visualization_specification.tsv
The first line specifies the version this file and the files referenced adhere to. The current version number is 1. The second line references the parameter file. This is followed by a list of (sub-)problems, in this case only one, referencing the respective condition, measurement observable, model, and visualization files. There can be multiple of those files, e.g. for large numbers of measurements, one could split those up into separate files, e.g. by experimental condition or observable.
6. Model simulation¶
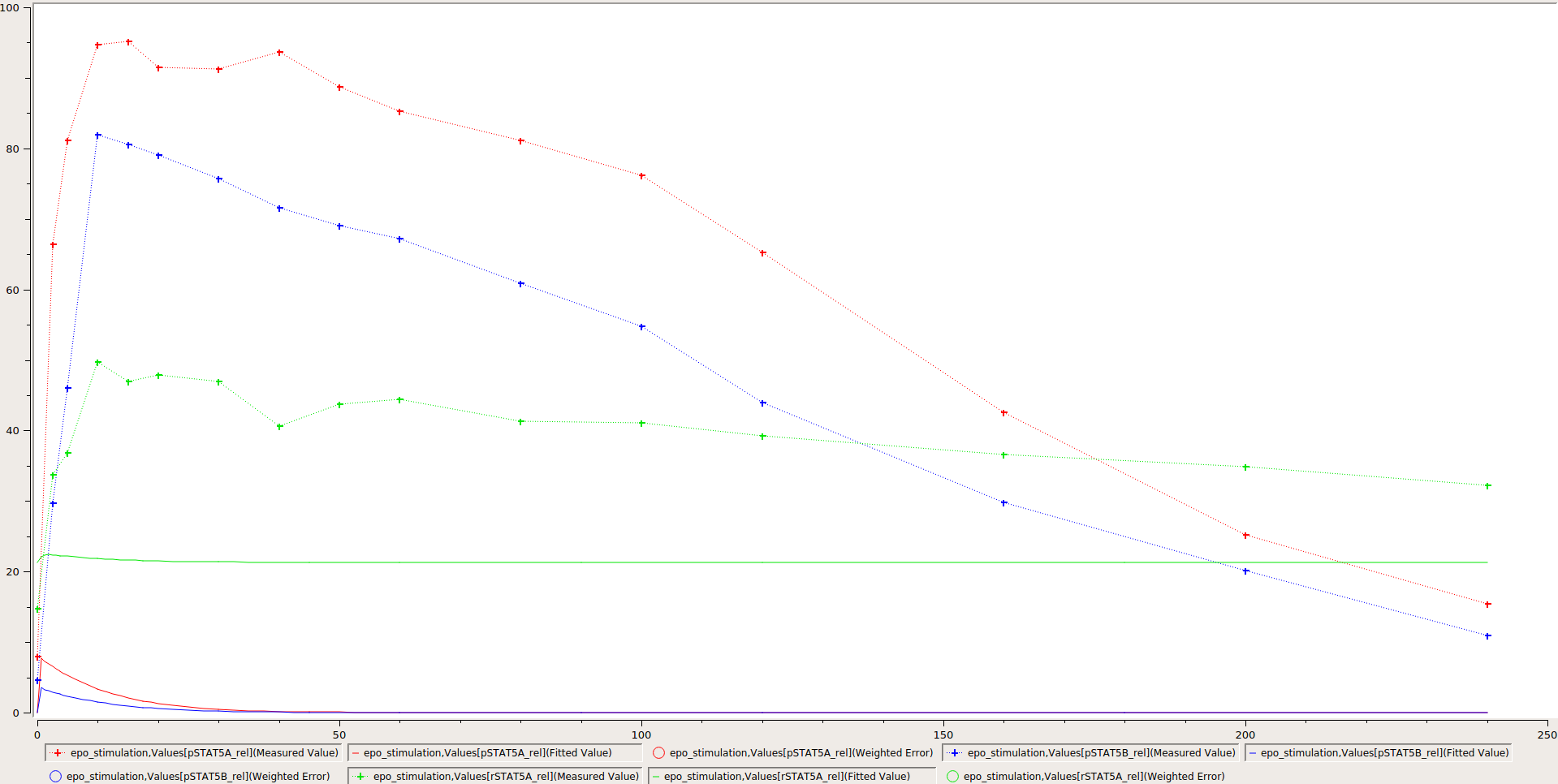
To simulate the model and compare it to the experimental data, the nominal parameters in the parameters file need to be set. As some parameters are a priori unknown, we here consider randomly sampled parameters to get a glance of model behaviour and fit to the data.
| parameterId | parameterScale | lowerBound | upperBound | nominalValue | estimate |
|---|---|---|---|---|---|
| Epo_degradation_BaF3 | log10 | 1E-5 | 1E+5 | 0.105 | 1 |
| k_exp_hetero | log10 | 1E-5 | 1E+5 | 1.85 | 1 |
| k_exp_homo | log10 | 1E-5 | 1E+5 | 9.83 | 1 |
| k_imp_hetero | log10 | 1E-5 | 1E+5 | 1048.96 | 1 |
| k_imp_homo | log10 | 1E-5 | 1E+5 | 10.136 | 1 |
| k_phos | log10 | 1E-5 | 1E+5 | 10.136 | 1 |
| ratio | lin | 0.693 | 0 | ||
| sd_pSTAT5A_rel | log10 | 1E-5 | 1E+5 | 51.7 | 1 |
| sd_pSTAT5B_rel | log10 | 1E-5 | 1E+5 | 0.257 | 1 |
| sd_rSTAT5A_rel | log10 | 1E-5 | 1E+5 | 0.017 | 1 |
With this, the model can be simulated using the different tools that support PEtab. The easiest tool to get started with is probably COPASI which comes with a graphical user interface (see https://github.com/copasi/python-petab-importer for further instructions).
It is apparent from the figure, that the random parameters yield a poor fit of the model with the data. Therefore, it is important to optimize the parameters to improve the model fit. This can be done using various parameter estimation tools. Links to detailed descriptions how to use the individual toolboxes are provided at the PEtab Github page.
7. Further information¶
This tutorial only demonstrates a subset of PEtab functionality. For full reference, consult the PEtab reference. After finishing the implementation of the PEtab problem, its correctness can be verified using the PEtab library (see https://github.com/PEtab-dev/PEtab/blob/master/doc/example/example_petablint.ipynb for instructions). The PEtab problem can then be used as input to the supporting toolboxes to estimate the unknown parameters or calculate parameter uncertainties. Links to tutorials for the different tools can be found at the PEtab Github page (https://github.com/PEtab-dev/PEtab#petab-support-in-systems-biology-tools).
| [1] | TSV files can be created using any standard spreadsheet application, or for small files, text editor. |